Dạy toán cho trẻ ở phương Tây: “tập hợp hóa” số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 2)

Năm 1959, hội nghị Royaumont về tư duy mới trong toán học diễn ra tại Pháp nêu yêu cầu cải cách dạy toán theo hệ thống cấu trúc toán học của trường phái Bourbaki và nghiên cứu tâm lý của Jean Piaget. Sau hội nghị, phong trào "Toán học Mới" hay "Toán Hiện đại" bùng nổ đã thay đổi chương trình môn toán từ đại học đến phổ thông ở Mỹ và nhiều nước châu Âu.

Một trong những cải cách của Toán học Mới là dạy số và 4 phép tính cho học sinh tiểu học dựa trên những khái niệm trừu tượng của thuyết tập hợp.;

Dùng thuyết tập hợp để dạy số và 4 phép tính là như thế nào? Chủ trương của các nhà cải cách Toán học Mới có thành công như mong đợi? Mời bạn đọc đến với phần 2: "Tập hợp hóa" các con số và 4 phép tính trong sách toán tiểu học thời Toán học Mới 1950-1980

Dạy toán cho trẻ ở phương tây: "tập hợp hóa" số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 1)

Con người có năng khiếu toán bẩm sinh, có tư duy về số từ 2 tuổi

"Công nghệ" dạy toán mới trên thế giới: khám phá quy tắc đại số trước khi đếm 1, 2, 3, 4... - phần 2

Bạn có thể hiểu sai ý nghĩa của các con số nếu nói "2 + 3 = 10" như GS Hồ Ngọc Đại

(Ảnh: Math worksheet 4 kids)

Bundgaard, định nghĩa mới về số và các phép toán

Bundgaard là bộ sách toán tiểu học chung của khối Bắc Âu thể hiện rõ nét chủ trương dạy số học theo tập hợp trong phong trào Toán học Mới những năm 1950-1980.

4 nước Bắc Âu Na Uy, Thụy Điển, Đan Mạch, Phần Lan đều là những quốc gia có nền giáo dục tiên tiến hàng đầu thế giới và nhiều năm liền đạt kết quả cao trong các kỳ kiểm tra đánh giá năng lực PISA (bài kiểm tra quốc tế nổi tiếng về năng lực học sinh ở độ tuổi 15 của OECD). Kết quả PISA gần nhất là PISA 2015 về cả 3 lĩnh vực toán, khoa học và đọc hiểu của 4 nước này đều đạt điểm trên trung bình so với khối OECD.

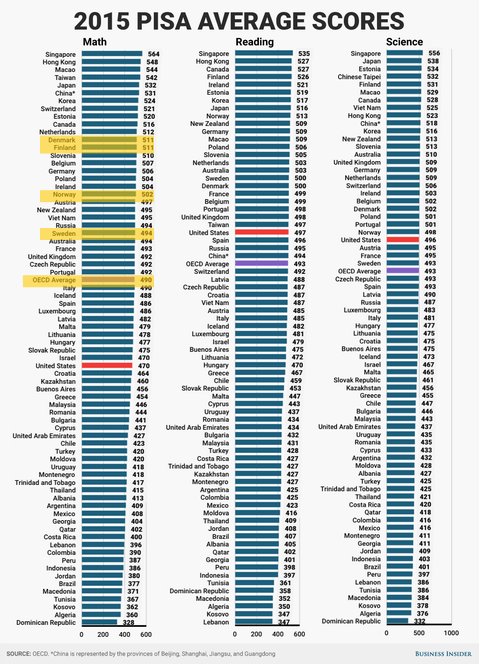
Điểm PISA gần nhất là PISA 2015 của 4 nước Bắc Âu Na Uy, Thụy Điển, Đan Mạch, Phần Lan đều đạt trên trung bình so với khối OECD (Ảnh: Business Insider)

Trước khi đi đến những thành quả trên, các nước Bắc Âu đã nhiều lần cải cách giáo dục, và Toán học Mới là một trong số đó. Trong xu thế đổi mới chương trình phổ thông từ 2020, bài học kinh nghiệm mang tên Toán học Mới ở các nước phương Tây cách đây gần nửa thế kỷ vẫn rất có giá trị tham khảo cho các nhà giáo dục và các phụ huynh nước ta.

Đan Mạch, nước có kết quả PISA 2015 môn toán cao nhất trong khối Bắc Âu và đứng thứ 7 trong khối OECD, là một trong các quốc gia hưởng ứng Toán học Mới mạnh mẽ nhất. "Cải cách toàn bộ chương trình và hiện đại hóa nó" là tuyên bố ủng hộ Toán học Mới của Svend Bundgaard, một đại biểu của Đan Mạch tại hội nghị Royaumont 1959. Sven Bundgaard (1912-1984) là giáo sư toán nổi tiếng ở đại học Aarhus và là một trong những diễn viên gây ảnh hưởng đến phong trào Toán học Mới tại Đan Mạch.

4 nước Na Uy, Thụy Điển, Đan Mạch, Phần Lan đã cùng hợp tác thành lập Ủy ban Bắc Âu về Dạy Toán Hiện đại (NKMM) gồm các nhà toán học, giáo viên toán, lãnh đạo trường học. Trực thuộc Ủy ban Văn hóa của Hội đồng Bắc Âu, NKMM hoạt động từ 1960 đến 1967, quản lý việc dạy toán ở các nước Bắc Âu trong phần lớn thập niên 1960.

Ủy ban NKMM cũng biên soạn các sách giáo khoa toán chung cho 4 nước Bắc Âu theo đúng tư tưởng Bourbaki và định hướng mà nhà toán học Gustave Choquet đã trình bày tại hội nghị Royaumont. Bộ sách toán cho cấp tiểu học 7-12 tuổi (tuổi học tiểu học ở Bắc Âu) do các giáo viên Đan Mạch thực hiện hoàn thành năm 1966 được đặt tên Bundgaard.

Bundgaard được thí điểm ở Đan Mạch và một nước Bắc Âu khác là Iceland. Iceland là một nước nhỏ thuộc lãnh thổ Đan Mạch mãi đến năm 1944 mới giành được độc lập. Tuy không tham gia ủy ban NKMM nhưng trước ảnh hưởng của OEEC (tổ chức hợp tác kinh tế châu Âu, tiền thân của OECD) và nguy cơ bị tụt hậu về giáo dục trên trường quốc tế, Iceland cũng hưởng ứng Toán học Mới. Quốc gia này đã "nhập khẩu", biên dịch và thí điểm bộ sách Bundgaard từ Đan Mạch.

Theo lời nhà sử học toán người Đan Mạch Jens Høyrup, bộ sách giáo khoa toán tiểu học Bundgaard của Bắc Âu là "cải cách chính thống nhất trước các yêu cầu của hội nghị Royaumont".

Bundgaard được biên soạn theo tinh thần Toán học Mới - toán hiện đại của Bourbaki và các lý thuyết tâm lý Jean Piaget mà nhà toán học Gustave Choquet đã trình bày tại hội nghị Royaumont: đề cao cấu trúc toán học trong toán hiện đại của trường phái Bourbaki, các nghiên cứu của Jean Piaget về mối liên hệ giữa cấu trúc trí óc và cấu trúc toán học, chú trọng phương pháp luận khám phá. Xin nhắc lại một số ý đã nêu trong phần 1 như dưới đây:

- Mục tiêu giảng dạy môn toán trong nhà trường có sự thay đổi theo hướng phát triển khái niệm và cách tư duy hơn là học thuộc lòng nên việc triển khai cũng thay đổi theo: sử dụng vật liệu cụ thể, xem việc học là kết quả của hiểu biết phát sinh từ khám phá hoặc thí nghiệm có hướng dẫn (guided experimentation or discovery).

(Ảnh: Youtube)

- Cách dạy số học truyền thống là học các con số và 4 phép tính căn bản như những sự kiện riêng lẻ. Trong Toán học Mới, trọng tâm cần nhấn mạnh là các khái niệm, ký hiệu tập hợp và khái niệm số dựa trên tập hợp, các tiên đề về trường số để hiểu rõ đặc điểm các phép toán mới.

- Theo phương pháp khám phá, để đi tới định nghĩa số là sự trừu tượng hóa đặc điểm của một tập hợp, học sinh phải được dẫn dắt đi từ một vài ý tưởng của thuyết tập hợp như: tập hợp, tập hợp con, sự tương ứng một-một, thứ tự. Do đó, môn toán lớp 1 bắt đầu bằng những khái niệm này rồi mới đến khái niệm số. Tập hợp dùng để dạy trẻ các khái niệm tương ứng một-một, hàm số, chuyển đổi và bằng nhau là tập hợp số nguyên.

Tập hợp số nguyên (Z) là một nhóm dưới phép cộng, là một vành đối với phép cộng và phép nhân thông thường. Tập hợp số nguyên cũng là một trường tương ứng với phép cộng và phép nhân thông thường. Nhóm, vành, trường là 3 dạng cấu trúc đại số cơ bản trong môn đại số trừu tượng.

- Chương trình số học trong trường tiểu học có thể đưa thêm các nội dung số thứ tự, số đếm hữu hạn, các khái niệm tập hợp con, phần bù tập hợp, hợp và giao của hai hoặc ba tập hợp. Phép cộng sẽ được trình bày là hợp của các tập hợp hữu hạn không có phần tử chung, phép nhân là tích của các tập hợp hữu hạn.

Dưới đây là phần so sánh Bundgaard với các bộ sách toán tiểu học tại Iceland trước và sau Toán học Mới. Nội dung và các hình minh họa được trích từ một nghiên cứu liên quan đăng tải trong báo cáo của hội nghị quốc tế về lịch sử giáo dục toán lần thứ 4 (the fourth International Conference On The History of Mathematics Education-ICHME-4) vào tháng 9 năm 2015 tại đại học Turin, Ý.

So với các sách giáo khoa trước đó thì Bundgaard có thêm các khái niệm của thuyết tập hợp, được bổ sung rải rác ở từng cấp lớp: tương ứng 1-1, tập hợp con cho học sinh lớp 1, hợp của tập hợp cho học sinh lớp 1 đến lớp 4, giao của tập hợp, nhập môn đại số tập hợp, hiệu và phần bù tập hợp ở lớp 4. 

Cách dạy toán theo cấu trúc toán hiện đại Bourbaki mà nhà toán học Gustave Choquet đề xướng tại Royaumont được phản ánh rất rõ trong Bundgaard, như hình 1 và 2 bên dưới:

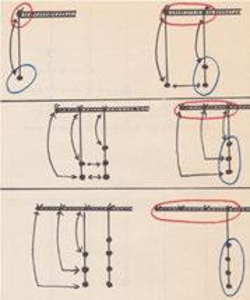
Hình 1: Khái niệm số trong sách giáo khoa Bundgaard lớp 1 được xây dựng bằng sự tương ứng một-một với trục số. Trục số được minh họa bằng các nút thắt

Hình 2: Thiết lập sự bằng nhau giữa hai tập hợp trong Bundgaard lớp 4

Khái niệm thứ tự được dạy bằng một số ví dụ đơn giản như hình 3 dưới đây. Hình này thể hiện quan điểm của Jean Piaget: dạy tập hợp con sẽ tạo ra một cấu trúc đại số sơ bộ giúp trẻ hiểu sâu ý niệm về sự bao gồm bộ phận-toàn thể (ví dụ tất cả hoa màu đỏ cũng đều là hoa).

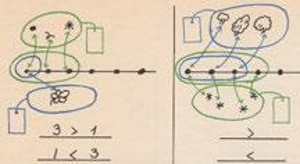
Hình 3: Tập hợp con và thứ tự trong Bundgaard lớp 1

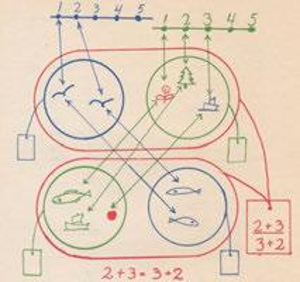
Phép cộng và nhân theo tập hợp như hình 4 và 5: phép cộng được dạy là hợp của các tập hợp hữu hạn không có phần tử chung, phép nhân là tích của các tập hợp hữu hạn. 

Hình 4: Phép cộng và trừ dựa trên tập hợp trong Bundgaard lớp 2

Hình 5: Phép nhân dựa trên tập hợp trong Bundgaard lớp 2

Thanh Cuisenaire là đồ dùng dạy học để minh họa các khái niệm số đếm, số thứ tự, tập hợp con… nói trên. Năm 1945, nhà giáo người Bỉ Emile-Georges Cuisenaire sáng chế ra bộ thanh gỗ gồm các khúc gỗ dài ngắn nhiều màu khác nhau được đặt theo tên ông Cuisenaire để dạy các con số và số học cơ bản. Cuisenaire được giới thiệu tại Pháp năm 1953, phổ biến tại Anh, Mỹ những năm 1950 và nổi tiếng trên thế giới từ đó.

(Ảnh: National Museum of American History)

Bundgaard cũng dạy cho học sinh các tiên đề về số sớm hơn các giáo trình cũ: luật (tính chất) giao hoán và kết hợp của phép cộng ở lớp 1, luật giao hoán của phép nhân, luật phân phối ở lớp 3, luật kết hợp của phép nhân và các hệ đếm khác ngoài hệ thập phân ở lớp 3.

Hình 6: Luật giao hoán, phép cộng và ký hiệu "+" trong Bundgaard lớp 1

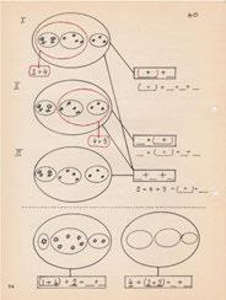
Hình 7: Luật kết hợp của phép cộng trong Bundgaard lớp 1

Hình 8: Luật phân phối trong Bundgaard lớp 2

Nhà sử học toán Jens Høyrup nhận xét Bundgaard đã "gây một số phiền toái cho các giáo viên lẫn phụ huynh". Theo báo cáo, Bundgaard cũng không thực hiện được mục tiêu khuyến khích sự khám phá hay thí nghiệm theo định hướng ban đầu. Trái lại, Bundgaard quá chú trọng tới ngôn ngữ tập hợp và thuyết tập hợp.

Trong các sách giáo khoa toán tiểu học sau Bundgaard ở Bắc Âu, ý định của phong trào cải cách là tập trung vào cấu trúc hệ thống số và việc dạy số theo các khái niệm của thuyết tập hợp đã dần biến mất.

Trong SFG, bộ sách giáo khoa toán tiểu học chính thức của Iceland từ 1971 - 2000, một số khái niệm mới về tập hợp trong Bundgaard đã không còn xuất hiện: phép hợp và giao, nhập môn đại số tập hợp, hiệu và phần bù tập hợp, ký hiệu, mod, logic biểu tượng (symbolism), chỉ còn lại 3 khái niệm mới là tập hợp, tập hợp con, tương ứng 1-1. Những khái niệm mới khác về số như các hệ thống module và hệ đếm khác hệ 10 trong Bundgaard cũng không có mặt trong SFG.

Đến bộ sách giáo khoa tiếp theo của Iceland là GP từ 1999-2010 thì tập hợp con và tương ứng 1-1 cũng bị xóa bỏ, chỉ còn khái niệm tập hợp ở lớp 4 và phép hợp, phép giao trên tập hợp ở lớp 5.

Vai trò của các ký hiệu và khái niệm tập hợp, các tiên đề của trường số cũng thay đổi. Trong SFG và GP, chúng chỉ còn là công cụ hỗ trợ tính toán nhiều hơn là các cấu trúc trọng tâm để xây dựng khái niệm số một cách có hệ thống, để hiểu các phép toán như trong Bundgaard. Các quy luật phân phối, kết hợp và giao hoán của phép nhân và phép cộng ở lớp 1 và 3 trong Bundgaard cũng được đưa lên các lớp 4, 5, 6 trong SFG và GP.

Bộ sách toán tiểu học Bundgaard là một ví dụ tiêu biểu cho cách dạy khái niệm số và 4 phép tính ở các nước phương Tây tham gia Toán học Mới những năm 1950-1980. Nhóm Bourbaki quy tụ những nhà toán học rất giỏi, hệ thống toán hiện đại Bourbaki đã có những đóng góp quan trọng cho sự phát triển của toán học, Jean Piaget là một trong những nhà tâm lý lớn nhất thế kỷ 20 nhưng chủ trương đổi mới việc dạy toán ở Mỹ và châu Âu theo tư tưởng Bourbaki và lý thuyết tâm lý Jean Piaget đã thất bại.

Toán học Mới theo tư tưởng Bourbaki-Jean Piaget đã thất bại như thế nào?

Năm 1970, nhà toán học Jean Dieudonné (đã được nhắc đến trong phần 1), một thành viên Bourbaki tham gia sáng lập CIEAEM (Ủy ban Quốc tế về Nghiên cứu và Cải tiến Giảng dạy Toán) và ủy ban cải cách Toán học Mới của Pháp, rút khỏi ủy ban cải cách.

Các sách toán thay thế Bundgaard cho thấy tham vọng cải cách của Toán học Mới không đạt kết quả.

Ở 4 nước lớn trong khối Bắc Âu đã thành lập NKMM, Na Uy chỉ thảo luận về Toán học Mới ở các ủy ban, quốc hội, báo chí, thử nghiệm có kiểm soát chứ không triển khai trên toàn hệ thống giáo dục.

Tại Thụy Điển, khi nước này chính thức áp dụng Toán học Mới từ năm 1969 thì sách toán tiểu học cũng được cải cách với nhiều nội dung mới, bố cục mới so với bộ sách trước đó vào năm 1962. Có những mục hoàn toàn mới như máy điện toán, hàm số, xác suất và thống kê. Một số chủ đề trở thành mục con của những chủ đề số học và đại số trước đó như số tự nhiên, số thập phân, phương trình. Trọng tâm chương trình cũng thay đổi từ các bài tập tính toán sang hiểu rõ khái niệm để tính toán. Đầu những năm 1980, Thụy Điển lại cho ra đời bộ sách toán tiểu học mới với cách phát triển chương trình quay lại kiểu cũ năm 1962.

Tại Đan Mạch, một trong những nước ủng hộ Toán học Mới nhiệt tình nhất và theo đuổi nó từ 1958-1978, tình hình cũng tương tự.

Ở Iceland, việc thử nghiệm bộ Bundgaard cấp tiểu học đi xuống từ năm 1970. Năm 1971, các nhà cải cách ở Iceland xuất bản một bộ sách mới là SFG thay thế Bundgaard với các sửa đổi như đã nêu trên. Có thể nêu ra một số lý do khiến Bundgaard không thành công ở Iceland: khi tỉ lệ học sinh ở trường tiểu học học sách Bundgaard ngày càng lớn, các nhà lãnh đạo phong trào không đủ khả năng hướng dẫn các giáo viên không được đào tạo bài bản về toán. Phụ huynh, công chúng và cả giáo viên đều không hiểu được mục tiêu của Toán học Mới.

Cách dạy số dựa trên các khái niệm trừu tượng của thuyết tập hợp bị phản đối, các sách giáo khoa mới thay thế đều quay lại cách dạy số theo truyền thống cũ là xu hướng chung ở Mỹ, Anh, Pháp và các nước khác tham gia Toán học Mới.

Ảnh tư liệu một lớp học ở Mỹ thời Toán học Mới (Ảnh: Conversation)

Quay lại truyền thống cũ, các nước dạy khái niệm số cho học sinh như thế nào? Các nhà thần kinh học nói gì về năng khiếu học số của con người chúng ta? Những câu hỏi này sẽ được giải đáp trong phần 3 (cũng là phần cuối), mời bạn đọc đón xem.

Tài liệu tham khảo:

1. Morten Friis Møller, 16/02/2017, Nordic PISA performance: Positive trend with warning signs, https://www.norden.org/en/news/nordic-pisa-performance-positive-trend-warning-signs

2. Kristín Bjarnadóttir (2017), Recommendations of the Royaumont Seminar on primary school arithmetic. Influences in the Nordic countries, "Dig where your stand" 4: Proceedings of the fourth international conference on the History of Mathematics Education, tr.51-58. Xem tại https://www.researchgate.net/publication/319781200_2017_-_Dig_where_you_stand_4_Proceedings_of_the_Fourth_International_Conference_on_the_History_of_Mathematics_Education, 

3. Kristín Bjarnadóttir (2013), The implementation of the ‘New Math' in Iceland: comparison to its neighboring countries, International Journal for the History of Mathematics Education, 8(1), tr.6, 8, 10, 14. Xem tại http://uni.hi.is/krisbj/files/2010/11/Vol8No1_Implrmrntation.pdf

4. Hans Christian Hansen (2009), From descriptive history to interpretation and explanation – a wave model for the development of mathematics education in Denmark, "Dig where you stand". Proceedings of the conference "On-going research in the History of Mathematics Education", tr.7. Xem tại https://skemman.is/bitstream/1946/26925/9/Hansen.pdf

5. Cuisenaire rods, https://americanhistory.si.edu/collections/search/object/nmah_694608

6. Numbers In Colour, A New Method of Teaching Arithmetic In Primary Schools, https://americanhistory.si.edu/collections/search/object/nmah_904659

Linh Trần (tổng hợp)