Dạy toán cho trẻ ở phương Tây: “tập hợp hóa” số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 4)

Tất cả hoa hồng đều là hoa nhưng không phải hoa nào cũng là hoa hồng. Theo Jean Piaget, phải đến 7 tuổi trẻ em mới hiểu được điều này, còn trước đó các em sẽ gặp khó khăn trong việc so sánh các tập hợp con và tập hợp mẹ của chúng trong tự nhiên. Jean Piaget là một trong những nhà tâm lý lớn nhất thế kỷ 20 nhưng ý kiến này của ông có vẻ rất ngớ ngẩn. Lẽ nào con em chúng ta lại "kém thông minh" đến mức 7 tuổi mới hiểu nổi một điều đơn giản như vậy?

Jean Piaget đúng hay trẻ nhỏ thông minh hơn ông đã nghĩ?;Mời bạn đọc theo dõi phần cuối của loạt bài 4 phần về chủ trương "tập hợp hóa" số học trong môn toán tiểu học ở phương Tây trong thế kỷ 20:

Trẻ mẫu giáo có khả năng xử lý dữ liệu tốt hơn các nhà khoa học từng nghĩ. 

Dạy toán cho trẻ ở phương tây: "tập hợp hóa" số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 1)

Dạy toán cho trẻ ở phương Tây: "tập hợp hóa" số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 2)

Dạy toán cho trẻ ở phương Tây: "tập hợp hóa" số học theo Jean Piaget-Bourbaki là một sai lầm (kỳ 3)

Con người có năng khiếu toán bẩm sinh, có tư duy về số từ 2 tuổi

"Công nghệ" dạy toán mới trên thế giới: khám phá quy tắc đại số trước khi đếm 1, 2, 3, 4... - phần 2

Chủ nghĩa kiến tạo (constructivism) do nhà tâm lý Jean Piaget đề xướng ra đời những năm 1950 có ảnh hưởng lớn đến các lý thuyết về cách học ở trẻ em và các hệ thống giáo dục hiện nay. Tuy vậy, thuyết kiến tạo về phát triển nhận thức ở trẻ em (children cognitive development) của Piaget có một số quan điểm không chính xác về năng lực toán học. Cùng với hệ thống cấu trúc toán học trừu tượng của nhóm Bourbaki, những quan điểm sai lầm của Piaget đã góp phần gây nên thảm họa "toán học mới" ở phương Tây giai đoạn 1950-1980.

(Ảnh: HRDevelopmentInfo)

Trẻ nhỏ trước tuổi lên 7 cần học tập hợp mới hiểu sâu ý nghĩa các con số và học tập hợp con để hiểu được quan hệ giữa một nhóm vật thể và các nhóm con. 2 quan điểm này của Jean Piaget được chú ý bởi chúng gắn liền các cấu trúc trí óc với hệ thống cấu trúc toán học trừu tượng của nhóm Bourbaki, một nhóm các nhà toán học lỗi lạc đến từ nước Pháp. Những lý thuyết toán học hiện đại và tâm lý của nhóm Bourbaki-Jean Piaget thời đó đã chi phối mạnh mẽ các nhà giáo dục phương Tây, khiến họ đưa tập hợp, tập hợp con vào chương trình toán tiểu học thời Toán học Mới.

Những "cải tiến" nêu trên đã biến mất sau khi Toán học Mới thất bại. Ý tưởng dạy số theo tập hợp đã được thảo luận trong 3 phần đầu. Ý tưởng về quan hệ bộ phận-toàn thể sẽ là trọng tâm của bài viết này.

Khái niệm sự bao hàm lớp (class inclusion) hay quan hệ bộ phận-toàn thể, quan hệ giữa nhóm, lớp và nhóm con, lớp con nghĩa là tất cả thành viên của một nhóm cũng đều thuộc về nhóm lớn hơn nhóm đó. Ví dụ, tất cả các hoa có màu đỏ đều là hoa.

Theo Jean Piaget, trẻ trước tuổi lên 7 không hiểu được điều đơn giản là tất cả hoa hồng đều là hoa nhưng không phải hoa nào cũng là hoa hồng.

Quan sát của Jean Piaget đến từ thí nghiệm sau: Người lớn đưa cho trẻ một bó hoa có 4 bông hoa màu đỏ và 2 hoa màu trắng rồi hỏi chúng: Có nhiều hoa hồng hơn hay nhiều hoa hơn?

Các trẻ lên năm, sáu luôn trả lời là nhiều hoa hồng hơn.

Do đó, Jean Piaget kết luận là, trẻ em ở giai đoạn tiền thao tác (preoperational stage, từ 2-7 tuổi) gặp khó khăn trong việc hiểu rõ khái niệm một lớp có nhiều lớp con. Mỗi lúc chúng chỉ tập trung vào một khía cạnh là lớp hoặc lớp con. Chỉ đến khi chúng có thể so sánh các bộ phận với toàn thể tạo nên các bộ phận cùng lúc thì chúng mới hiểu được mối quan hệ giữa lớp và lớp con, còn gọi là tư duy bao hàm lớp (class inclusion reasoning).

Bài toán bao hàm lớp của Jean Piaget: Are there more roses or more flowers? (Có nhiều hoa hồng hơn hay nhiều hoa hơn?)

Cũng như thí nghiệm về nguyên tắc bảo toàn số ở trẻ, thí nghiệm về sự bao hàm lớp của Jean Piaget đã được các nhà nghiên cứu sau ông kiểm nghiệm lại và cho ra những kết quả khác hẳn.

Theo Parenting Science, cách đặt câu hỏi của Jean Piaget hơi kỳ lạ. Trong cuộc sống hàng ngày, chúng ta không hỏi "có nhiều hoa đỏ hay nhiều hoa hơn". Có khả năng là nhiều trẻ chưa bao giờ được hỏi một câu như thế.

Do đó, khi gặp câu hỏi lạ này, có thể đứa trẻ sẽ suy luận, người lớn không nói theo nghĩa đen. Có thể người lớn thật sự đang hỏi mình so sánh hoa đỏ với hoa trắng.

Các nghiên cứu khác đã thay đổi cách dùng ngôn ngữ khi đặt câu hỏi về tập hợp cho trẻ. Ví dụ như 2 câu sau:

- Đây là một chùm nho. Có những quả nho xanh và quả nho tím, và đây là chùm nho.

- Ai sẽ có nhiều nho hơn để ăn, người ăn nho xanh hay người ăn cả chùm nho?

Đây là một cách đặt vấn đề tự nhiên hơn. Và nó đã tạo nên sự khác biệt. Khi được hỏi những câu theo "ngôn ngữ tự nhiên" này, số trẻ trả lời đúng cao hơn đáng kể, theo nghiên cứu của Markman và Seibert công bố năm 1976.

Một nghiên cứu của nhóm James McGarrigle (đại học Edinburgh, Anh) năm 1978 với các trẻ 6 tuổi cũng cho thấy, khi thay đổi cách hỏi, tỉ lệ trẻ trả lời đúng tăng lên. James đưa ra 4 con bò mô hình, ba con đen và một con trắng. Cả 4 con được đặt sang một phía, trông như chúng đang ngủ.

Các trẻ tham gia được hỏi 2 câu:

- Có nhiều bò đen hơn hay nhiều bò hơn?

- Có nhiều bò đen hơn hay nhiều bò đang ngủ hơn?

Kết quả là số trẻ trả lời đúng câu 1 chỉ có 25%, nhưng câu 2 là 48%.

Như vậy, trẻ em có khả năng hiểu được sự bao hàm lớp sớm hơn quan điểm của Jean Piaget. Cách đặt câu hỏi của Piaget là trở ngại cho các trẻ nhỏ hơn trong việc chứng minh chúng hiểu được quan hệ lớp và lớp con.

Nhiều nghiên cứu khác cũng đi theo hướng đặt ra những câu hỏi có ý nghĩa rõ ràng hơn, tránh sự mơ hồ. Kết quả là khả năng các trẻ tham gia thí nghiệm trả lời sai giảm đi nhiều khi người lớn điều chỉnh lại cách dùng từ, theo một công trình của nhà tâm lý Guy Politzer (học viện Institut Jean Nicod, Pháp) năm 2016.

(Ảnh: The Dreme Network)

Ngoài ra, các nhà nghiên cứu cũng chứng minh được năng lực của trẻ em với tập hợp trong những nhiệm vụ hoàn toàn mới. Các trẻ 4-5 tuổi đã làm tốt thử thách phân loại một nhóm đồ chơi hỗn hợp thành nhóm mẹ gồm các loài động vật và hai nhóm con là các con nhỏ và lớn trong cùng loài. Không chỉ vậy, chúng còn mở rộng ý tưởng, phân loại luôn cả những vật thể khác như các hình khối và bong bóng. Đây là kết quả một nghiên cứu về tư duy bao hàm lớp của hai nhà tâm lý phát triển Usha Goswami (đại học Cambridge, Anh quốc) và Sabina Pauen (đại học Heidelberg, Đức).

Kỹ năng phân loại là khả năng xác định các đặc điểm của một nhóm, liên hệ nhóm/lớp này với nhóm/lớp kia và sử dụng thông tin phân loại để giải quyết vấn đề. Một trong những thành phần của kỹ năng phân loại là 2 khả năng: nhóm các vật thể theo một số đặc điểm chung, sắp xếp các nhóm con của một nhóm theo cấp bậc sao cho mỗi nhóm mới đều bao gồm các nhóm con trước đó.

Theo tiêu chuẩn năng lực cốt lõi chung (Common Core Standards) môn toán của Mỹ, phân loại các vật thể theo nhóm, đếm số lượng và sắp xếp các nhóm theo số lượng là kỹ năng cần có về dữ liệu (Data) với trẻ mẫu giáo lớn (grade K, 5-6 tuổi).

Dưới đây là một bài tập phân loại, sắp xếp và đếm số dành cho trẻ học lớp mẫu giáo lớn ở Mỹ:

(Ảnh: Planning Play time)

Tiêu chuẩn CCSS cho thấy, kết luận từ các nghiên cứu mới nêu trên đã được các nhà giáo dục phương Tây thừa nhận và áp dụng thay cho quan điểm sai lầm cách đây hơn nửa thế kỷ của Jean Piaget.

Trẻ nhỏ có nhiều tiềm năng toán học hơn các nhà tâm lý từng nghĩ về chúng!

Về mặt sinh học, vấn đề có thể nằm ở chỗ thùy trán (frontal cortex, frontal lobe) là cơ quan đảm trách "điều hành trung ương". Thùy trán chưa trưởng thành khiến trẻ không thể ngăn cản một xu hướng tự phát nhưng sai lầm. Khiếm khuyết này là lý do trẻ trả lời sai câu hỏi của Jean Piaget: trong một bó 8 hoa gồm 6 hoa hồng, 2 hoa tulip thì số hoa hồng nhiều hơn số hoa.

Ngoài ra, sự trẻ con cũng có thể là triệu chứng cho thấy vỏ não trước trán thiếu khả năng giám sát hành vi. Vỏ não trước trán (prefrontal cortex) là bộ phận điều khiển và duy trì sự tập trung và lý trí, giúp con người hiểu được bản thân mình và người khác.

Trên đây là lý giải của nhà thần kinh học nhận thức Stanislas Dehaene trong cuốn The Number Sense (đã được trích dẫn khá nhiều trong phần 3) về các bộ phận của não ảnh hưởng đến khả năng tư duy, nhận thức của con người.

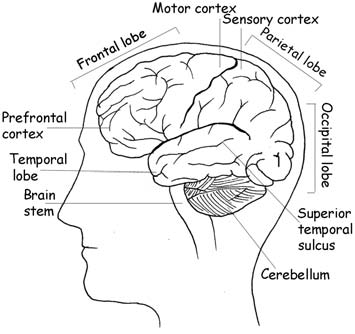
Cấu tạo bộ não (Ảnh trong The Number Sense)

Tài liệu tham khảo:

1. Dehaene, S. (1999). The Number Sense: How the mind creates mathematics. New York: Oxford University Press, tr.202.

2. Dewar, G (2019). Are kids smarter than they appear? Parenting Science. Xem tại

https://www.parentingscience.com/cognitive-development.html

3. McLeod, S. A. (2018, Jan 14). Concrete operational stage. Simply Psychology. Xem tại https://www.simplypsychology.org/concrete-operational.html

4. Lan T (24/12/2014), Thiền có thể thay đổi cấu trúc não bộ, xem tại https://www.facebook.com/notes/clb-t%C3%A2m-l%C3%BD-h%E1%BB%8Dc/thi%E1%BB%81n-c%C3%B3-th%E1%BB%83-thay-%C4%91%E1%BB%95i-c%E1%BA%A5u-tr%C3%BAc-n%C3%A3o-b%E1%BB%99/926802257360774/

5. Interpreting inclusion: A contribution to the study of the child's cognitive and linguistic development https://www.sciencedirect.com/science/article/abs/pii/0022096578901315

Linh Trần (tổng hợp)