VNR Content
Pearl
Leonardo Fibonacci là một nhà toán học ở Pisa, Ý. Khoảng năm 1202, ông đề ra một bài toán liên quan tới các chú thỏ.
Giả sử ta có một cặp thỏ mắn đẻ, cuối mỗi tháng lại sinh ra một cặp mới, mỗi cặp mới cũng đẻ sau một tháng và không có con nào chết. Vậy sau một năm ta có bao nhiêu cặp thỏ?
Để tính được con số này, Fibonacci đã giải như sau:
Gọi F
Ta có F
Ta thấy ở đầu tháng thứ n thì các cặp có thể chia thành hai nhóm: nhóm cặp “cũ” đã có sau n-1 tháng là F
Kết quả là:
F
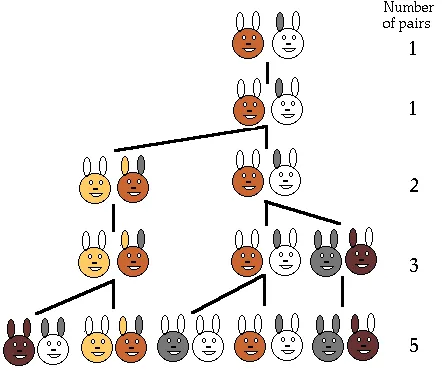
(Ảnh: Dr Ron Knott)
Sử dụng công thức này và các giá trị ban đầu F
Dãy số Fibonacci chính là chuỗi các số F
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Bài toán này đã được Fibonacci nhắc tới trong cuốn sách “Liber Abaci” (Một cuốn sách về các phép toán) dành cho các thương nhân, trình bày các phép toán số học Ả rập-Ấn Độ hữu ích để theo dõi lời lỗ, cán cân nợ còn lại.
Leonardo Fibonacci được xem là một trong những nhà toán học giỏi nhất thời trung cổ. Dãy số Fibonacci xuất hiện trong mọi lĩnh vực toán học và cả trong tự nhiên. Dãy Fibonacci liên quan chặt chẽ đến tỉ số vàng (phi, φ). Tỉ số vàng phi là một số hữu tỉ có giá trị 1.6180339887498948482..., được tính theo công thức sau:
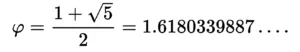 Tỉ số vàng có thể phản ánh sự phát triển của một số loại cây cỏ. Ví dụ, cách sắp xếp hình xoắn ốc của lá hoặc cánh hoa của một số loại cây như cây thông, các hạt hoa hướng dương tuân theo mô hình dãy Fibonacci và tỉ số vàng.
Tỉ số vàng có thể phản ánh sự phát triển của một số loại cây cỏ. Ví dụ, cách sắp xếp hình xoắn ốc của lá hoặc cánh hoa của một số loại cây như cây thông, các hạt hoa hướng dương tuân theo mô hình dãy Fibonacci và tỉ số vàng.
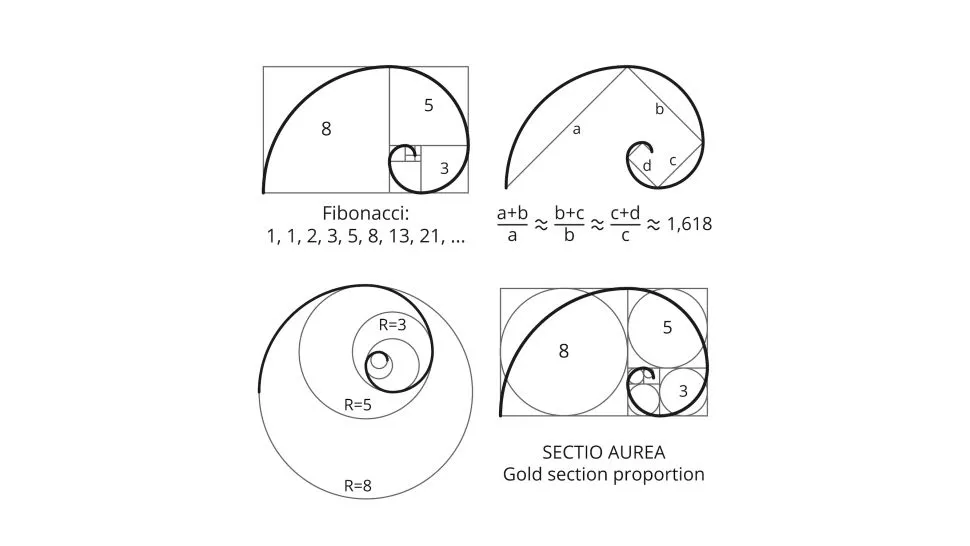 Các minh họa dãy Fibonacci và tỉ số vàng (Ảnh: Shutterstock)
Các minh họa dãy Fibonacci và tỉ số vàng (Ảnh: Shutterstock)
 Dãy số Fibonacci là mô hình của hình xoắn ốc màu vàng ở các hạt trong hoa hướng dương (Ảnh: Getty Images)
Dãy số Fibonacci là mô hình của hình xoắn ốc màu vàng ở các hạt trong hoa hướng dương (Ảnh: Getty Images)
Theo Math Fun Facts, Live Science
Giả sử ta có một cặp thỏ mắn đẻ, cuối mỗi tháng lại sinh ra một cặp mới, mỗi cặp mới cũng đẻ sau một tháng và không có con nào chết. Vậy sau một năm ta có bao nhiêu cặp thỏ?
Để tính được con số này, Fibonacci đã giải như sau:
Gọi F
n là số cặp thỏ ở đầu tháng thứ n.Ta có F
1=1, F2=2 vì đầu tháng thứ nhất ta có một cặp ban đầu, đầu tháng thứ hai thì ta có hai cặp do cặp đầu tiên đẻ ra thêm cặp thứ hai.Ta thấy ở đầu tháng thứ n thì các cặp có thể chia thành hai nhóm: nhóm cặp “cũ” đã có sau n-1 tháng là F
n-1, nhóm cặp “mới” vừa được sinh ra thêm. Số lượng cặp mới bằng tổng số các cặp của hai tháng trước Fn-2, do mỗi cặp mới sẽ đẻ sau một tháng và đẻ ra cháu đầu tiên sau một tháng nữa.Kết quả là:
F
n=Fn-1+Fn-2
(Ảnh: Dr Ron Knott)
Sử dụng công thức này và các giá trị ban đầu F
1=1 và F2=2, số cặp thỏ ta có sau một năm là F12=233 cặp.Dãy số Fibonacci chính là chuỗi các số F
n. Theo quy định, các giá trị ban đầu thường được chọn là 0 và 1, hoặc 1 và 1:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Bài toán này đã được Fibonacci nhắc tới trong cuốn sách “Liber Abaci” (Một cuốn sách về các phép toán) dành cho các thương nhân, trình bày các phép toán số học Ả rập-Ấn Độ hữu ích để theo dõi lời lỗ, cán cân nợ còn lại.
Leonardo Fibonacci được xem là một trong những nhà toán học giỏi nhất thời trung cổ. Dãy số Fibonacci xuất hiện trong mọi lĩnh vực toán học và cả trong tự nhiên. Dãy Fibonacci liên quan chặt chẽ đến tỉ số vàng (phi, φ). Tỉ số vàng phi là một số hữu tỉ có giá trị 1.6180339887498948482..., được tính theo công thức sau:
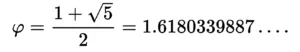


>>> Tiêu chuẩn "Tỷ lệ vàng" khuôn mặt xuất phát từ đâu, liệu có cơ sở khoa học ?
Theo Math Fun Facts, Live Science