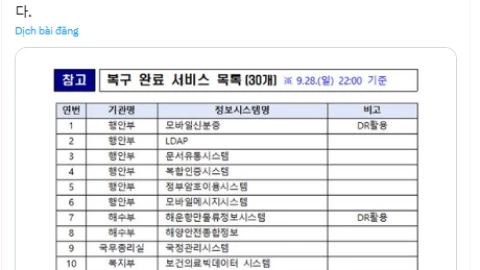
VNR Content
Pearl
Chúng ta đã biết rằng, có nhiều bộ ba Pythagore, là các nhóm ba số nguyên thỏa mãn
Ví dụ
Nhưng liệu có bộ ba nào thỏa mãn
với các lũy thừa n là số nguyên lớn hơn 2?
Nhà toán học, luật sư người Pháp Pierre de Fermat tuyên bố rằng câu trả lời là không. Năm 1637, ông nguệch ngoạc bên lề một cuốn sách đang đọc (tác giả là Diophantus) là ông có “một chứng minh thật sự tuyệt vời cho giả thuyết này, nhưng lề sách quá hẹp để viết vào”.
Không tồn tại các nghiệm nguyên x, y và z khác 0 thỏa mãn
khi n là một số nguyên lớn hơn 2, phát biểu thu hút này trở nên nổi tiếng và được gọi là định lý cuối cùng của Fermat mặc dù nó vẫn chỉ là một phỏng đoán, bởi vì Fermat chưa bao giờ tiết lộ “chứng minh” của ông cho bất kỳ ai.
Nhiều trường hợp đặc biệt đã được đặt ra, ví dụ như các trường hợp trong các lũy thừa đặc biệt, các gia đình lũy thừa trong các trường hợp đặc biệt. Tuy nhiên, trong hàng thế kỷ bài toán tổng quát vẫn chưa được giải quyết. Nhiều bộ óc xuất sắc đã tìm kiếm chứng minh cho phỏng đoán này nhưng đều thất bại.
Mãi đến năm 1993, nhà toán học người Anh Andrew Wiles sau nhiều năm theo đuổi bài toán đã khám phá ra một cách chứng minh dựa trên một liên hệ với lý thuyết đường cong elip. Dù chứng minh này có một lỗ hổng, đến năm 1994 Wiles và Richard Taylor đã sửa được nó. Và cuối cùng, giả thuyết của Fermat đã trở thành một “định lý”!
Định lý Fermat cuối cùng đã được nhà toán học Andrew Wiles tìm ra cách giải (Ảnh: CNN)
Trong địa hạt toán học, việc theo đuổi bài toán này và những vấn đề liên quan đã mở ra những lĩnh vực mới về lý thuyết số và liên kết nó với các lĩnh vực khác, chẳng hạn như lý thuyết đường cong elip. Wiles đặt nền tảng công trình của mình dựa trên một kết quả của Ken Ribet năm 1986 cho thấy giả thuyết Taniyama-Shimura trong hình học số học/đại số chỉ ra định lý cuối cùng của Fermat.
Wiles có thể chứng minh giả thuyết Taniyama-Shimura, giả thuyết đặt ra một cuốn “từ điển” giữa đường cong elip và các dạng mô đun (module) bằng cách biến đổi các đường cong elip thành các biểu diễn Galois (Galois representations). Cách tư duy này đã đem lại những kỹ thuật mới để giải quyết bài toán chưa có lời giải trong hơn 300 năm.
Một vấn đề là, với chiều sâu của các kỹ thuật cần thiết để dẫn tới chứng minh này, nhiều người cho rằng Fermat đã tưởng nhầm khi nghĩ rằng ông đã tìm ra một cách chứng minh.
Nhờ Andrew Wiles mà định lý Fermat nổi tiếng làm đau đầu nhiều nhà toán học sau hơn 300 năm đã có lời giải. Công trình chứng minh định lý Fermat đã giúp nhà toán học Andrew Wiles được vinh danh trong nhiều giải thưởng lớn: Fermat Prize năm 1995, đĩa bạc (Silver Plaque) của Liên đoàn Toán học Quốc tế năm 1998, giải Abel năm 2016, huy chương Copley của Hội Hoàng gia Luân Đôn năm 2017. Đặc biệt nhất trong số này là giải Abel của Viện Hàn lâm Khoa học Na Uy, được xem là giải Nobel toán học, giải thưởng danh giá nhất thế giới cho ngành toán học. Giá trị giải thưởng Abel mà nhà toán học Wiles nhận được lên đến 700.000 USD (6 triệu krone Na Uy).
Theo Math Fun Facts
Ví dụ
Nhưng liệu có bộ ba nào thỏa mãn
Nhà toán học, luật sư người Pháp Pierre de Fermat tuyên bố rằng câu trả lời là không. Năm 1637, ông nguệch ngoạc bên lề một cuốn sách đang đọc (tác giả là Diophantus) là ông có “một chứng minh thật sự tuyệt vời cho giả thuyết này, nhưng lề sách quá hẹp để viết vào”.
Không tồn tại các nghiệm nguyên x, y và z khác 0 thỏa mãn
Nhiều trường hợp đặc biệt đã được đặt ra, ví dụ như các trường hợp trong các lũy thừa đặc biệt, các gia đình lũy thừa trong các trường hợp đặc biệt. Tuy nhiên, trong hàng thế kỷ bài toán tổng quát vẫn chưa được giải quyết. Nhiều bộ óc xuất sắc đã tìm kiếm chứng minh cho phỏng đoán này nhưng đều thất bại.
Mãi đến năm 1993, nhà toán học người Anh Andrew Wiles sau nhiều năm theo đuổi bài toán đã khám phá ra một cách chứng minh dựa trên một liên hệ với lý thuyết đường cong elip. Dù chứng minh này có một lỗ hổng, đến năm 1994 Wiles và Richard Taylor đã sửa được nó. Và cuối cùng, giả thuyết của Fermat đã trở thành một “định lý”!
Trong địa hạt toán học, việc theo đuổi bài toán này và những vấn đề liên quan đã mở ra những lĩnh vực mới về lý thuyết số và liên kết nó với các lĩnh vực khác, chẳng hạn như lý thuyết đường cong elip. Wiles đặt nền tảng công trình của mình dựa trên một kết quả của Ken Ribet năm 1986 cho thấy giả thuyết Taniyama-Shimura trong hình học số học/đại số chỉ ra định lý cuối cùng của Fermat.
Wiles có thể chứng minh giả thuyết Taniyama-Shimura, giả thuyết đặt ra một cuốn “từ điển” giữa đường cong elip và các dạng mô đun (module) bằng cách biến đổi các đường cong elip thành các biểu diễn Galois (Galois representations). Cách tư duy này đã đem lại những kỹ thuật mới để giải quyết bài toán chưa có lời giải trong hơn 300 năm.
Một vấn đề là, với chiều sâu của các kỹ thuật cần thiết để dẫn tới chứng minh này, nhiều người cho rằng Fermat đã tưởng nhầm khi nghĩ rằng ông đã tìm ra một cách chứng minh.
Nhờ Andrew Wiles mà định lý Fermat nổi tiếng làm đau đầu nhiều nhà toán học sau hơn 300 năm đã có lời giải. Công trình chứng minh định lý Fermat đã giúp nhà toán học Andrew Wiles được vinh danh trong nhiều giải thưởng lớn: Fermat Prize năm 1995, đĩa bạc (Silver Plaque) của Liên đoàn Toán học Quốc tế năm 1998, giải Abel năm 2016, huy chương Copley của Hội Hoàng gia Luân Đôn năm 2017. Đặc biệt nhất trong số này là giải Abel của Viện Hàn lâm Khoa học Na Uy, được xem là giải Nobel toán học, giải thưởng danh giá nhất thế giới cho ngành toán học. Giá trị giải thưởng Abel mà nhà toán học Wiles nhận được lên đến 700.000 USD (6 triệu krone Na Uy).
>>> Liệu chúng ta có thể trở thành nhà toán học bằng con đường tự học (phần 1)
>>> Liệu chúng ta có thể trở thành nhà toán học bằng con đường tự học (phần 2)
>>> Liệu chúng ta có thể trở thành nhà toán học bằng con đường tự học (phần 3)
Theo Math Fun Facts
