Ngọc Yến
Writer
Cuộc sống đầy rẫy những quyết định lớn, và việc đưa ra lựa chọn giữa những lựa chọn dường như vô tận có thể là – ừm, khó khăn đến tê liệt. Bạn nên mua căn hộ này, hay căn hộ kia? Chia sẻ với người bạn cùng nhà này, hay người khác? Chọn anh chàng Đẹp-Đẹp-Tuyệt-Vời, hay chờ đợi xem anh chàng Hoàn-hảo có xuất hiện không?
Đủ để khiến bạn tuyệt vọng – nhưng đừng sợ: khoa học có giải pháp. Vâng, toán học có , ít nhất là như vậy.

Tối ưu hóa các tùy chọn của bạn
Giống như một số lượng lớn các thông tin toán học đáng ngạc nhiên khác, thông tin này nổi tiếng là một câu đố "giải trí" do Martin Gardner đặt ra (tất nhiên, các câu đố còn lại do John Conway đặt ra ).
Vào năm 1960, câu đố này được đưa ra dưới dạng "Bài toán thư ký" và diễn ra như sau : bạn cần thuê một thư ký; có n ứng viên cần phỏng vấn, được chấp nhận hoặc từ chối, theo thứ tự ngẫu nhiên; bạn có thể xếp hạng họ theo mức độ phù hợp mà không có sự ràng buộc nào; một khi đã bị từ chối, ứng viên sẽ không thể được gọi lại; cuối cùng, tất cả hoặc không có gì - bạn sẽ không hài lòng với ứng viên đứng thứ tư hoặc thứ hai ở đây.
Các thiết lập khác bao gồm "bài toán hôn phu" (cùng ý tưởng, nhưng bạn đang tìm một vị hôn phu thay vì một thư ký) và "trò chơi googol" - trong phiên bản đó, bạn sẽ lật các tờ giấy để lộ ra các con số cho đến khi bạn quyết định rằng có lẽ bạn đã tìm thấy con số lớn nhất.
Dù bạn chơi theo cách nào thì câu hỏi vẫn như vậy: làm thế nào để tối đa hóa khả năng chọn được phương án tốt nhất?
Câu trả lời là… hóa ra lại dễ đoán đến ngạc nhiên.
Quy tắc 37 phần trăm
Viết ra bằng lời, đây là một vấn đề phức tạp và khó hiểu. Trong toán học, nó khá đơn giản.
“Vấn đề cơ bản này có một giải pháp đơn giản đáng kinh ngạc”, nhà toán học và thống kê Thomas S Ferguson đã viết vào năm 1989. “Đầu tiên, người ta chỉ ra rằng sự chú ý có thể được giới hạn vào lớp các quy tắc mà đối với một số nguyên r > 1 nào đó thì từ chối r – 1 ứng viên đầu tiên , và sau đó chọn ứng viên tiếp theo tốt nhất trong thứ hạng tương đối của các ứng viên được quan sát”.
Vì vậy, khi đối mặt với một loạt các lựa chọn ngẫu nhiên và muốn chọn ra lựa chọn tốt nhất được đưa ra cho bạn, điều đầu tiên bạn phải làm là… từ chối tất cả mọi người. Nghĩa là, cho đến một điểm nào đó – và khi bạn đạt đến điểm đó, chỉ cần chấp nhận ứng viên, người theo đuổi hoặc tờ giấy tiếp theo, đánh bại mọi thứ bạn đã thấy cho đến nay.
Câu hỏi bây giờ rất đơn giản: khi nào bạn đạt đến điểm đó?
Vâng, giả sử điểm dừng là ứng viên thứ m – mọi người cho đến lúc đó đều bị từ chối. Bây giờ, nếu ứng viên tốt nhất là ( m +1), xin chúc mừng, bạn sẽ chấp nhận họ và có được người được tuyển dụng tốt nhất có thể.
Nhưng nếu ứng viên tốt nhất là ( m + 2) thì sao? Vâng, khi đó chúng ta có hai cách để giải quyết vấn đề này: hoặc là ( m + 1) tốt hơn m đầu tiên , nhưng không phải là tốt nhất có thể, trong trường hợp đó thật không may – bạn không có được ứng viên tốt nhất, vì bạn đã chọn người tiền nhiệm của họ – hoặc bạn từ chối ( m + 1) và chấp nhận ( m + 2).
Bây giờ, tất nhiên, chúng ta muốn kịch bản thứ hai, không phải kịch bản thứ nhất – vì vậy, đây là một số tin tốt: trong tất cả các sắp xếp của ứng viên đầu tiên ( m +1), chỉ có 1/( m +1) kịch bản mà bạn sẽ chấp nhận ( m +1) chứ không phải ( m +2). Điều đó có nghĩa là vẫn còn m /( m +1) kịch bản mà bạn giữ vững và nhận được những điều tốt nhất.
Được rồi, vậy thì sao nếu ứng viên tốt nhất đang ngồi ở ( m +3)? Vâng, họ chỉ được chấp nhận nếu không có ứng viên ( m +1) hay ứng viên ( m +2) nào đánh bại được tất cả những người trước họ – và điều đó chỉ xảy ra trong 2/( m +2) trường hợp. Một lần nữa, điều đó có nghĩa là bạn chờ đợi những người tốt nhất trong m /( m +2) trường hợp.
Có lẽ bạn đã thấy một mô hình rồi: nhìn chung, nếu ứng viên thứ n là người giỏi nhất, họ sẽ được chấp nhận m /( n – 1) lần trong tổng số ( n – 1).
Khi chúng ta để n tăng đến vô cực, mô hình này trở thành một giới hạn. “Xác suất, ϕ( r ), để chọn ứng viên tốt nhất là 1/ n đối với r = 1,” Ferguson giải thích, “và, đối với r > 1 […] tổng trở thành một phép xấp xỉ Riemann đối với một tích phân,
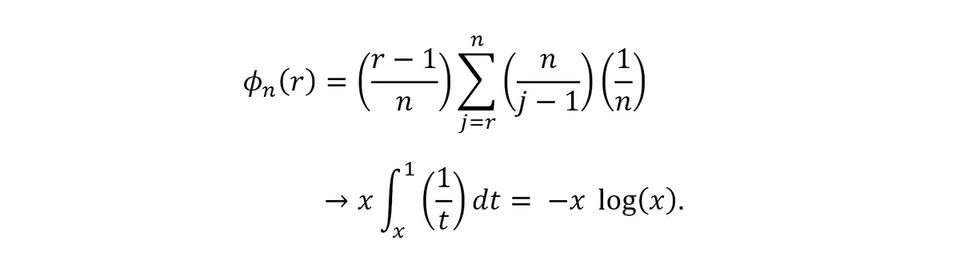
Bây giờ câu hỏi là: làm thế nào để chúng ta tối đa hóa giá trị đó? Và câu trả lời thực sự khá đơn giản: bạn đặt x là 1/ e , tức là khoảng 0,368.
Do cách thức hoạt động của logarit và số mũ, điều này có nghĩa là ϕ( r ) = 0,367879… cũng vậy. Nói cách khác, “gần như tối ưu khi đợi cho đến khi khoảng 37% số ứng viên được phỏng vấn và sau đó chọn ứng viên tốt nhất tiếp theo”, Ferguson giải thích. “Xác suất thành công cũng vào khoảng 37%”.
Điều đó có vẻ không thực sự ấn tượng - xét cho cùng, nó chỉ hơn một phần ba cơ hội bạn sẽ tìm thấy lựa chọn tốt nhất có thể. Nhưng khi bạn cân nhắc đến phương án thay thế, thì thật khó tin: "Nếu bạn chọn không theo chiến lược này và thay vào đó chọn ổn định cuộc sống với một đối tác ngẫu nhiên, bạn sẽ chỉ có 1/ n cơ hội tìm thấy tình yêu đích thực của mình, hoặc chỉ 5 phần trăm nếu bạn được định sẵn sẽ hẹn hò với 20 người trong suốt cuộc đời, chẳng hạn", Hannah Fry , Giáo sư về Hiểu biết công chúng về Toán học tại Đại học Cambridge, đã viết trong cuốn sách năm 2015 của bà có tên là Toán học của tình yêu: Các mô hình, bằng chứng và tìm kiếm phương trình tối thượng .
“Nhưng bằng cách từ chối 37 phần trăm người yêu đầu tiên và áp dụng chiến lược này, bạn có thể thay đổi vận mệnh của mình một cách đáng kể, lên tới 38,42 phần trăm cho một định mệnh với 20 người yêu tiềm năng.”
Nó có thực sự hiệu quả không?
Vậy là: 37 phần trăm. Không quan trọng bạn chọn gì; bạn có bao nhiêu lựa chọn; tất cả đều phụ thuộc vào tỷ lệ phần trăm cực kỳ quan trọng đó. Nghe có vẻ hơi quá tốt để có thể là sự thật, phải không?
“Tôi là một nhà toán học và do đó có thành kiến, nhưng kết quả này thực sự khiến tôi kinh ngạc,” Fry viết. “Bạn có ba tháng để tìm một nơi để sống? Hãy từ chối mọi thứ trong tháng đầu tiên và sau đó chọn ngôi nhà tiếp theo xuất hiện mà bạn thích nhất cho đến nay. Thuê một trợ lý? Hãy từ chối 37 phần trăm ứng viên đầu tiên và sau đó giao việc cho người tiếp theo mà bạn thích hơn tất cả những người khác.”
Vậy, nếu logic là hợp lý, và toán học kiểm tra - mà nó đã kiểm tra - tại sao kết quả này lại có vẻ sai đến vậy ? Vâng, như Fry đã chỉ ra trong một bài diễn thuyết Ted năm 2014 , có một số cờ lê thực tế có thể được ném vào: "phương pháp này đi kèm với một số rủi ro", cô nói; "Ví dụ, hãy tưởng tượng nếu đối tác hoàn hảo của bạn xuất hiện trong 37 phần trăm đầu tiên của bạn. Bây giờ, thật không may, bạn sẽ phải từ chối họ."
Nhưng "nếu bạn tính toán", bà nói tiếp, "tôi e rằng sẽ không có ai khác giỏi hơn bất kỳ ai bạn từng gặp trước đây, vì vậy bạn phải tiếp tục từ chối mọi người và chết trong cô độc".
Tuy nhiên, vẫn có một cách để tránh kết cục như mèo chow : hãy hạ thấp tiêu chuẩn của bạn xuống.
“Phép toán giả định rằng bạn chỉ quan tâm đến việc tìm kiếm người bạn đời tốt nhất có thể dành cho bạn,” Fry viết. “Nhưng […] trên thực tế, nhiều người trong chúng ta thích một người bạn đời tốt hơn là ở một mình nếu Người Ấy không có mặt.”
Vì vậy, chắc chắn, bạn có khoảng 37 phần trăm cơ hội tìm thấy Người Ấy bằng cách từ chối 37 phần trăm đầu tiên xuất hiện - nhưng nếu bạn ổn với việc chỉ tìm thấy Một trong 5 phần trăm hàng đầu thì sao? Vâng, trong trường hợp đó, điểm dừng của bạn thấp hơn: "nếu bạn từ chối những đối tác xuất hiện trong 22 phần trăm đầu tiên của khung thời gian hẹn hò của bạn và chọn người tiếp theo xuất hiện, người tốt hơn bất kỳ ai bạn từng gặp trước đây […] bạn sẽ ổn định với một người trong top 5 phần trăm những đối tác tiềm năng của bạn một cách ấn tượng 57 phần trăm thời gian", Fry giải thích.
Chấp nhận bất kỳ ai trong số 15 phần trăm đối tượng tiềm năng hàng đầu, và cơ hội của bạn sẽ tăng cao hơn nữa. Sau đó, bạn chỉ cần từ chối 19 phần trăm đầu tiên xuất hiện – và bạn có thể mong đợi cơ hội thành công gần bốn trong năm.
Và hãy nhìn nhận thực tế: khi nói đến tình yêu, những điều đó không phải là điều tệ . Dù sao thì vẫn tốt hơn chiêm tinh học.
Đủ để khiến bạn tuyệt vọng – nhưng đừng sợ: khoa học có giải pháp. Vâng, toán học có , ít nhất là như vậy.

Tối ưu hóa các tùy chọn của bạn
Giống như một số lượng lớn các thông tin toán học đáng ngạc nhiên khác, thông tin này nổi tiếng là một câu đố "giải trí" do Martin Gardner đặt ra (tất nhiên, các câu đố còn lại do John Conway đặt ra ).
Vào năm 1960, câu đố này được đưa ra dưới dạng "Bài toán thư ký" và diễn ra như sau : bạn cần thuê một thư ký; có n ứng viên cần phỏng vấn, được chấp nhận hoặc từ chối, theo thứ tự ngẫu nhiên; bạn có thể xếp hạng họ theo mức độ phù hợp mà không có sự ràng buộc nào; một khi đã bị từ chối, ứng viên sẽ không thể được gọi lại; cuối cùng, tất cả hoặc không có gì - bạn sẽ không hài lòng với ứng viên đứng thứ tư hoặc thứ hai ở đây.
Các thiết lập khác bao gồm "bài toán hôn phu" (cùng ý tưởng, nhưng bạn đang tìm một vị hôn phu thay vì một thư ký) và "trò chơi googol" - trong phiên bản đó, bạn sẽ lật các tờ giấy để lộ ra các con số cho đến khi bạn quyết định rằng có lẽ bạn đã tìm thấy con số lớn nhất.
Dù bạn chơi theo cách nào thì câu hỏi vẫn như vậy: làm thế nào để tối đa hóa khả năng chọn được phương án tốt nhất?
Câu trả lời là… hóa ra lại dễ đoán đến ngạc nhiên.
Quy tắc 37 phần trăm
Viết ra bằng lời, đây là một vấn đề phức tạp và khó hiểu. Trong toán học, nó khá đơn giản.
“Vấn đề cơ bản này có một giải pháp đơn giản đáng kinh ngạc”, nhà toán học và thống kê Thomas S Ferguson đã viết vào năm 1989. “Đầu tiên, người ta chỉ ra rằng sự chú ý có thể được giới hạn vào lớp các quy tắc mà đối với một số nguyên r > 1 nào đó thì từ chối r – 1 ứng viên đầu tiên , và sau đó chọn ứng viên tiếp theo tốt nhất trong thứ hạng tương đối của các ứng viên được quan sát”.
Vì vậy, khi đối mặt với một loạt các lựa chọn ngẫu nhiên và muốn chọn ra lựa chọn tốt nhất được đưa ra cho bạn, điều đầu tiên bạn phải làm là… từ chối tất cả mọi người. Nghĩa là, cho đến một điểm nào đó – và khi bạn đạt đến điểm đó, chỉ cần chấp nhận ứng viên, người theo đuổi hoặc tờ giấy tiếp theo, đánh bại mọi thứ bạn đã thấy cho đến nay.
Câu hỏi bây giờ rất đơn giản: khi nào bạn đạt đến điểm đó?
Vâng, giả sử điểm dừng là ứng viên thứ m – mọi người cho đến lúc đó đều bị từ chối. Bây giờ, nếu ứng viên tốt nhất là ( m +1), xin chúc mừng, bạn sẽ chấp nhận họ và có được người được tuyển dụng tốt nhất có thể.
Nhưng nếu ứng viên tốt nhất là ( m + 2) thì sao? Vâng, khi đó chúng ta có hai cách để giải quyết vấn đề này: hoặc là ( m + 1) tốt hơn m đầu tiên , nhưng không phải là tốt nhất có thể, trong trường hợp đó thật không may – bạn không có được ứng viên tốt nhất, vì bạn đã chọn người tiền nhiệm của họ – hoặc bạn từ chối ( m + 1) và chấp nhận ( m + 2).
Bây giờ, tất nhiên, chúng ta muốn kịch bản thứ hai, không phải kịch bản thứ nhất – vì vậy, đây là một số tin tốt: trong tất cả các sắp xếp của ứng viên đầu tiên ( m +1), chỉ có 1/( m +1) kịch bản mà bạn sẽ chấp nhận ( m +1) chứ không phải ( m +2). Điều đó có nghĩa là vẫn còn m /( m +1) kịch bản mà bạn giữ vững và nhận được những điều tốt nhất.
Được rồi, vậy thì sao nếu ứng viên tốt nhất đang ngồi ở ( m +3)? Vâng, họ chỉ được chấp nhận nếu không có ứng viên ( m +1) hay ứng viên ( m +2) nào đánh bại được tất cả những người trước họ – và điều đó chỉ xảy ra trong 2/( m +2) trường hợp. Một lần nữa, điều đó có nghĩa là bạn chờ đợi những người tốt nhất trong m /( m +2) trường hợp.
Có lẽ bạn đã thấy một mô hình rồi: nhìn chung, nếu ứng viên thứ n là người giỏi nhất, họ sẽ được chấp nhận m /( n – 1) lần trong tổng số ( n – 1).
Khi chúng ta để n tăng đến vô cực, mô hình này trở thành một giới hạn. “Xác suất, ϕ( r ), để chọn ứng viên tốt nhất là 1/ n đối với r = 1,” Ferguson giải thích, “và, đối với r > 1 […] tổng trở thành một phép xấp xỉ Riemann đối với một tích phân,
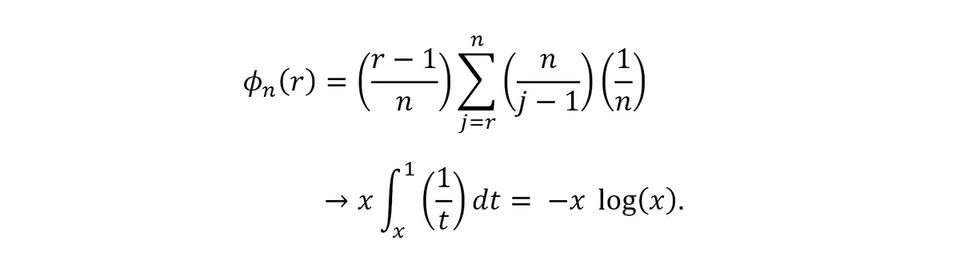
Bây giờ câu hỏi là: làm thế nào để chúng ta tối đa hóa giá trị đó? Và câu trả lời thực sự khá đơn giản: bạn đặt x là 1/ e , tức là khoảng 0,368.
Do cách thức hoạt động của logarit và số mũ, điều này có nghĩa là ϕ( r ) = 0,367879… cũng vậy. Nói cách khác, “gần như tối ưu khi đợi cho đến khi khoảng 37% số ứng viên được phỏng vấn và sau đó chọn ứng viên tốt nhất tiếp theo”, Ferguson giải thích. “Xác suất thành công cũng vào khoảng 37%”.
Điều đó có vẻ không thực sự ấn tượng - xét cho cùng, nó chỉ hơn một phần ba cơ hội bạn sẽ tìm thấy lựa chọn tốt nhất có thể. Nhưng khi bạn cân nhắc đến phương án thay thế, thì thật khó tin: "Nếu bạn chọn không theo chiến lược này và thay vào đó chọn ổn định cuộc sống với một đối tác ngẫu nhiên, bạn sẽ chỉ có 1/ n cơ hội tìm thấy tình yêu đích thực của mình, hoặc chỉ 5 phần trăm nếu bạn được định sẵn sẽ hẹn hò với 20 người trong suốt cuộc đời, chẳng hạn", Hannah Fry , Giáo sư về Hiểu biết công chúng về Toán học tại Đại học Cambridge, đã viết trong cuốn sách năm 2015 của bà có tên là Toán học của tình yêu: Các mô hình, bằng chứng và tìm kiếm phương trình tối thượng .
“Nhưng bằng cách từ chối 37 phần trăm người yêu đầu tiên và áp dụng chiến lược này, bạn có thể thay đổi vận mệnh của mình một cách đáng kể, lên tới 38,42 phần trăm cho một định mệnh với 20 người yêu tiềm năng.”
Nó có thực sự hiệu quả không?
Vậy là: 37 phần trăm. Không quan trọng bạn chọn gì; bạn có bao nhiêu lựa chọn; tất cả đều phụ thuộc vào tỷ lệ phần trăm cực kỳ quan trọng đó. Nghe có vẻ hơi quá tốt để có thể là sự thật, phải không?
“Tôi là một nhà toán học và do đó có thành kiến, nhưng kết quả này thực sự khiến tôi kinh ngạc,” Fry viết. “Bạn có ba tháng để tìm một nơi để sống? Hãy từ chối mọi thứ trong tháng đầu tiên và sau đó chọn ngôi nhà tiếp theo xuất hiện mà bạn thích nhất cho đến nay. Thuê một trợ lý? Hãy từ chối 37 phần trăm ứng viên đầu tiên và sau đó giao việc cho người tiếp theo mà bạn thích hơn tất cả những người khác.”
Vậy, nếu logic là hợp lý, và toán học kiểm tra - mà nó đã kiểm tra - tại sao kết quả này lại có vẻ sai đến vậy ? Vâng, như Fry đã chỉ ra trong một bài diễn thuyết Ted năm 2014 , có một số cờ lê thực tế có thể được ném vào: "phương pháp này đi kèm với một số rủi ro", cô nói; "Ví dụ, hãy tưởng tượng nếu đối tác hoàn hảo của bạn xuất hiện trong 37 phần trăm đầu tiên của bạn. Bây giờ, thật không may, bạn sẽ phải từ chối họ."
Nhưng "nếu bạn tính toán", bà nói tiếp, "tôi e rằng sẽ không có ai khác giỏi hơn bất kỳ ai bạn từng gặp trước đây, vì vậy bạn phải tiếp tục từ chối mọi người và chết trong cô độc".
Tuy nhiên, vẫn có một cách để tránh kết cục như mèo chow : hãy hạ thấp tiêu chuẩn của bạn xuống.
“Phép toán giả định rằng bạn chỉ quan tâm đến việc tìm kiếm người bạn đời tốt nhất có thể dành cho bạn,” Fry viết. “Nhưng […] trên thực tế, nhiều người trong chúng ta thích một người bạn đời tốt hơn là ở một mình nếu Người Ấy không có mặt.”
Vì vậy, chắc chắn, bạn có khoảng 37 phần trăm cơ hội tìm thấy Người Ấy bằng cách từ chối 37 phần trăm đầu tiên xuất hiện - nhưng nếu bạn ổn với việc chỉ tìm thấy Một trong 5 phần trăm hàng đầu thì sao? Vâng, trong trường hợp đó, điểm dừng của bạn thấp hơn: "nếu bạn từ chối những đối tác xuất hiện trong 22 phần trăm đầu tiên của khung thời gian hẹn hò của bạn và chọn người tiếp theo xuất hiện, người tốt hơn bất kỳ ai bạn từng gặp trước đây […] bạn sẽ ổn định với một người trong top 5 phần trăm những đối tác tiềm năng của bạn một cách ấn tượng 57 phần trăm thời gian", Fry giải thích.
Chấp nhận bất kỳ ai trong số 15 phần trăm đối tượng tiềm năng hàng đầu, và cơ hội của bạn sẽ tăng cao hơn nữa. Sau đó, bạn chỉ cần từ chối 19 phần trăm đầu tiên xuất hiện – và bạn có thể mong đợi cơ hội thành công gần bốn trong năm.
Và hãy nhìn nhận thực tế: khi nói đến tình yêu, những điều đó không phải là điều tệ . Dù sao thì vẫn tốt hơn chiêm tinh học.