Thế Việt
Writer
Một bài toán hình học hóc búa đã thách thức các nhà toán học trong gần bốn thế kỷ, kể từ thời của nhà triết học và toán học vĩ đại người Pháp René Descartes, cuối cùng đã tìm được lời giải đáp. Các nhà nghiên cứu tại Đại học Monash (Australia) vừa công bố một bước đột phá quan trọng, khi sử dụng các công cụ toán học tiên tiến lấy cảm hứng từ vật lý lý thuyết để mở rộng Định lý Đường tròn nổi tiếng của Descartes sang một phạm vi hoàn toàn mới.
Những điểm chính
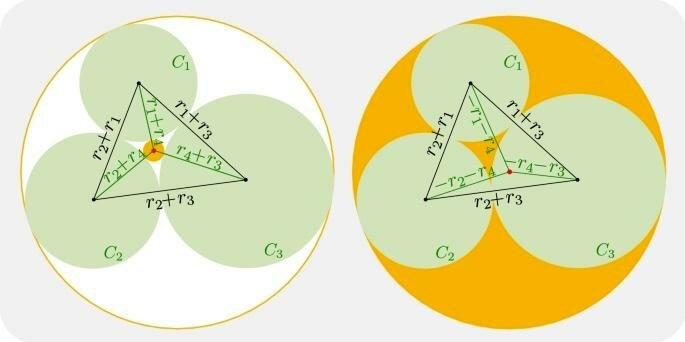
Định lý Đường tròn của Descartes, một nền tảng của hình học cổ điển, mô tả một cách thanh lịch mối quan hệ toán học giữa bốn đường tròn tiếp xúc ngoài lẫn nhau (thường được gọi là "nụ hôn của các đường tròn"). Tuy nhiên, việc tổng quát hóa định lý này để áp dụng cho một hệ thống gồm nhiều hơn bốn đường tròn tiếp tuyến đã là một trở ngại lớn, làm đau đầu các nhà toán học qua nhiều thế kỷ.
Giờ đây, nhóm nghiên cứu tại Monash, dẫn đầu bởi Tiến sĩ Orion Zymaris, đã thành công trong việc xây dựng một phương trình tổng quát áp dụng cho bất kỳ số lượng đường tròn tiếp tuyến nào. Điều đáng kinh ngạc là chìa khóa để giải quyết bài toán hình học cổ điển này lại đến từ một lĩnh vực tưởng chừng không liên quan: vật lý hiện đại.

Cụ thể, các nhà nghiên cứu đã sử dụng spinor – những thực thể toán học phức tạp thường được dùng để mô tả các thuộc tính trong cơ học lượng tử (như spin của hạt cơ bản) và trong thuyết tương đối. Nhóm đã áp dụng một phiên bản spinor đặc biệt được phát triển bởi hai nhà vật lý đoạt giải Nobel là Roger Penrose và Wolfgang Rindler, những người đã sử dụng chúng trong nghiên cứu về lý thuyết tương đối.
Việc ứng dụng thành công spinor vào bài toán đường tròn đã hé lộ một mối liên hệ sâu sắc và bất ngờ giữa các cấu trúc toán học mô tả thế giới lượng tử và cấu trúc không-thời gian với một vấn đề thuần túy hình học về sự sắp xếp của các đường tròn.
"Hóa ra, các cấu trúc toán học tương tự mô tả spin lượng tử và thuyết tương đối cũng giúp chúng ta hiểu được sự sắp xếp của các đường tròn," Tiến sĩ Orion Zymaris chia sẻ.
Phát hiện này không chỉ giải quyết một câu đố tồn tại gần 400 năm mà còn mang đến những hiểu biết mới mẻ, cho thấy sự thống nhất và vẻ đẹp tiềm ẩn trong các lĩnh vực khác nhau của toán học và vật lý. Nó chứng tỏ rằng đôi khi, những công cụ mạnh mẽ từ các ngành khoa học hiện đại có thể soi sáng và giải quyết những vấn đề tưởng chừng đã đi vào ngõ cụt của toán học cổ điển.

Những điểm chính
- Các nhà toán học tại Đại học Monash (Úc) đã tìm ra lời giải cho bài toán mở rộng Định lý Đường tròn Descartes, có tuổi đời gần 380 năm.
- Bài toán gốc của Descartes mô tả mối quan hệ của 4 đường tròn tiếp xúc nhau; bài toán mở rộng áp dụng cho bất kỳ số lượng đường tròn tiếp xúc nào.
- Lời giải đột phá này đạt được nhờ việc sử dụng công cụ toán học spinor, vốn thường được ứng dụng trong vật lý lượng tử và thuyết tương đối.
- Nhóm nghiên cứu đã sử dụng một phiên bản spinor đặc biệt do các nhà vật lý đoạt giải Nobel Penrose và Rindler phát triển.
- Kết quả nghiên cứu đã hé lộ một mối liên hệ sâu sắc và bất ngờ giữa các cấu trúc toán học của vật lý hiện đại và bài toán hình học cổ điển về sự sắp xếp các đường tròn.
Định lý Đường tròn của Descartes, một nền tảng của hình học cổ điển, mô tả một cách thanh lịch mối quan hệ toán học giữa bốn đường tròn tiếp xúc ngoài lẫn nhau (thường được gọi là "nụ hôn của các đường tròn"). Tuy nhiên, việc tổng quát hóa định lý này để áp dụng cho một hệ thống gồm nhiều hơn bốn đường tròn tiếp tuyến đã là một trở ngại lớn, làm đau đầu các nhà toán học qua nhiều thế kỷ.
Giờ đây, nhóm nghiên cứu tại Monash, dẫn đầu bởi Tiến sĩ Orion Zymaris, đã thành công trong việc xây dựng một phương trình tổng quát áp dụng cho bất kỳ số lượng đường tròn tiếp tuyến nào. Điều đáng kinh ngạc là chìa khóa để giải quyết bài toán hình học cổ điển này lại đến từ một lĩnh vực tưởng chừng không liên quan: vật lý hiện đại.

Cụ thể, các nhà nghiên cứu đã sử dụng spinor – những thực thể toán học phức tạp thường được dùng để mô tả các thuộc tính trong cơ học lượng tử (như spin của hạt cơ bản) và trong thuyết tương đối. Nhóm đã áp dụng một phiên bản spinor đặc biệt được phát triển bởi hai nhà vật lý đoạt giải Nobel là Roger Penrose và Wolfgang Rindler, những người đã sử dụng chúng trong nghiên cứu về lý thuyết tương đối.
Việc ứng dụng thành công spinor vào bài toán đường tròn đã hé lộ một mối liên hệ sâu sắc và bất ngờ giữa các cấu trúc toán học mô tả thế giới lượng tử và cấu trúc không-thời gian với một vấn đề thuần túy hình học về sự sắp xếp của các đường tròn.
"Hóa ra, các cấu trúc toán học tương tự mô tả spin lượng tử và thuyết tương đối cũng giúp chúng ta hiểu được sự sắp xếp của các đường tròn," Tiến sĩ Orion Zymaris chia sẻ.
Phát hiện này không chỉ giải quyết một câu đố tồn tại gần 400 năm mà còn mang đến những hiểu biết mới mẻ, cho thấy sự thống nhất và vẻ đẹp tiềm ẩn trong các lĩnh vực khác nhau của toán học và vật lý. Nó chứng tỏ rằng đôi khi, những công cụ mạnh mẽ từ các ngành khoa học hiện đại có thể soi sáng và giải quyết những vấn đề tưởng chừng đã đi vào ngõ cụt của toán học cổ điển.